
Albert Einstein once said “Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn’t, pays it”.
While some people question whether the quote was in fact from Einstein, the power of compound interest is unquestionable.
Who is credited with creating the concept of compound interest?
The Florentine merchant Francesco Balducci Pegolotti provided a table of compound interest in his book Pratica della mercatura of about 1340. It gives the interest on 100 lire, for rates from 1% to 8%, for up to 20 years.
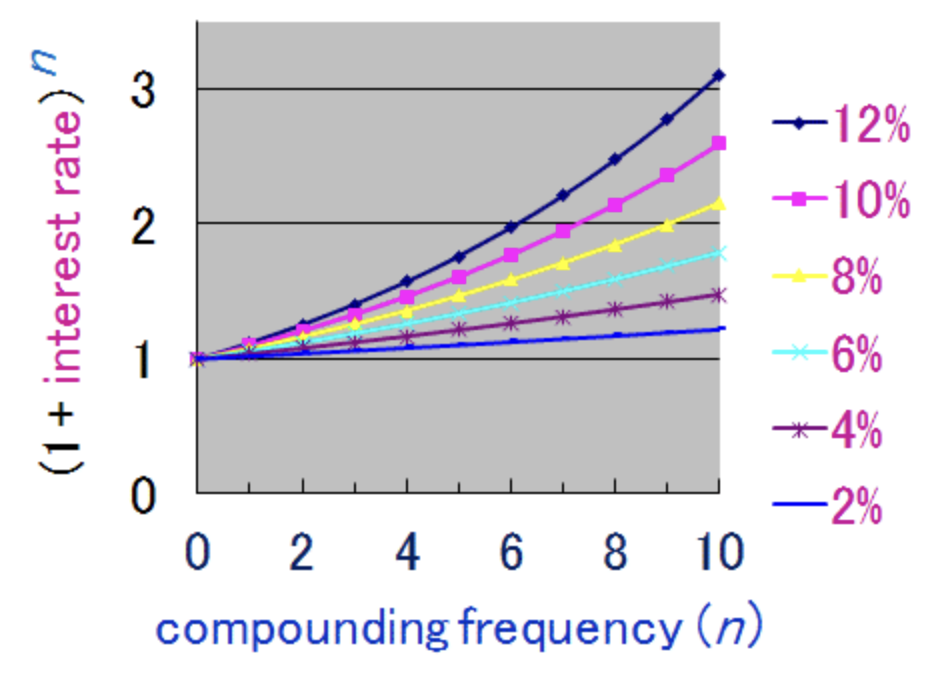
What exactly is compound interest?
According to Wikipedia: Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on principal plus interest. It is the result of reinvesting interest, or adding it to the loaned capital rather than paying it out, or requiring payment from borrower, so that interest in the next period is then earned on the principal sum plus previously accumulated interest. Compound interest is standard in finance and economics.
What’s the difference between simple and compound interest?
Compound interest is contrasted with simple interest, where previously accumulated interest is not added to the principal amount of the current period, so there is no compounding. The simple annual interest rate is the interest amount per period, multiplied by the number of periods per year. The simple annual interest rate is also known as the nominal interest rate (not to be confused with the interest rate not adjusted for inflation, which goes by the same name).
Compound interest allows money to make money. Interest earned is added to principal, and the combined amount now earns interest.
Why does it matter whether the interest is simple or compounded?
The difference between simple and compound interest matters a great deal because over time compound interest will generate much more money with the same initial principal invested. It does this because the interest earned is added to the principal and both earn more interest. With simple interest the accumulated interest is not added to the original principal.
Does compounding frequently make a difference?
Absolutely! The best deal would be an account the compounds daily (continuously.) Increasing frequency of compounding will increase the compounding of the principal. (Increasing frequency of compounding equals more money.)
The chart below illustrates the effects of different compounding periods on an initial $1,000.00 investment earning 20% annual interest.
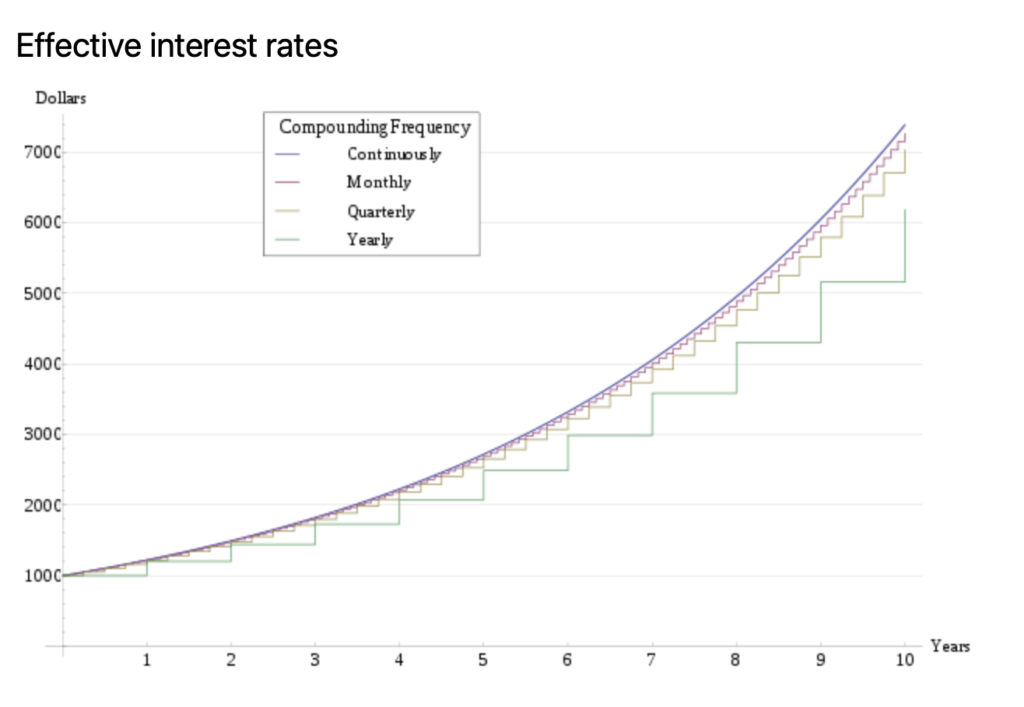
The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies.
Don’t confuse frequency of compounding with interest rates. Just like frequency of compounding, interest rates can be stated as a monthly, quarterly, or annual rate. (Buyer Beware: A 2% monthly interest rate surely sounds much more appealing than a 24% annual rate. Yet, they are the same rate. If the 2% rate is compounded monthly, it’s actually worse than a straight 24% annual rate.)
Personal loan interest is calculated using one of three methods – simple, compound, or add-on; with the simple interest method being the most common.
So, In referring to Einstein’s statement. If one understands the value of compounding, then compounding will work in your favor through compounding of investments. Conversely, if someone does not understand compounding then it works against them in the form of higher compounded loan interest.
Let’s look at an example:
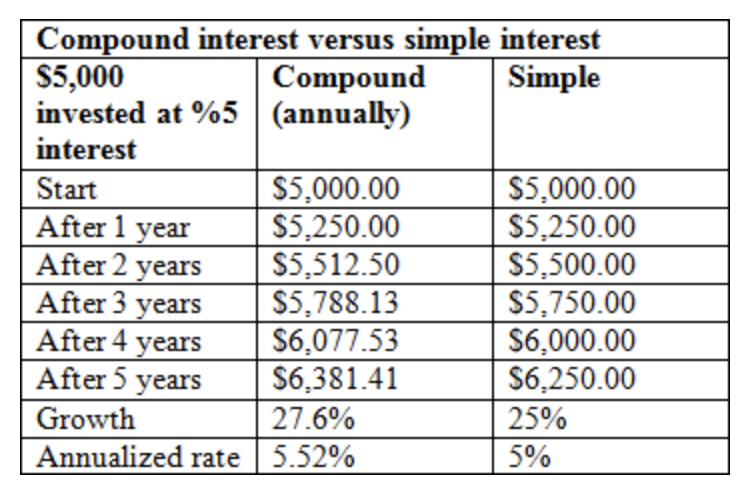
For example, if you had $5,000 in an account that paid 5% annually in simple interest for five years, you’d earn $250 a year, for a total of $1,250 in interest. In this case the interest rate and the yield are the same — 5% per year.
But the same $5,000 investment paying 5% interest compounded annually for five years would produce a total of $1,381.41 in interest. Because you’re earning interest on your interest, the yield — an average of 5.52% per year — is higher than the interest rate.
How does the time horizon of investments affect Compound Interest?
According to an AMG funds article:
For Compound Interest to work, it requires three things: the original investment remain invested, the reinvestment of earnings, and time. The more time you give your investments, the more you may be able to accelerate the income potential of your original investment.
To demonstrate, let’s look at another example:
If you invest $10,000 and it returns 6%, you will have $10,600 in one year ($10,000 x 1.06). Rather than withdraw the $600 gained, you keep it in there for another year. If you continue to earn the same rate of 6%, your investment will grow to $11,236 ($10,600 x 1.06) by the end of the second year.
Because you reinvested that $600, it works together with the original investment, earning you $636, which is $36 more than the previous year. This little bit extra may seem like peanuts now, but do not forget that you did not have to lift a finger to earn that $36. More importantly, this $36 also has the capacity to earn interest. After the next year, assuming the same 6% return, your investment would be worth $11,910 ($11,236 x 1.06). This time you earned $674, which is $74 more than the first year. This increase in the amount made each year is compounding in action: investment earnings on investment earnings and so on. This has the potential to continue, assuming you keep invested and investment returns are positive.
Kate Ashford provided the following information in a Forbes Advisor article:
The Simple Interest formula:
A = P (1 + [r / n]) ^ nt
- A = the amount of money accumulated after n years, including interest
- P = the principal amount (your initial deposit or your initial credit card bill)
- r = the annual rate of interest (as a decimal)
- t = the number of years (time) the amount is deposited for
Compound Interest Formula Excel
You can calculate compound interest in Microsoft Excel using the Future Value (FV) financial function:
=FV(rate,nper,pmt,[pv],[type])
- FV = future value
- rate = the interest rate per period
- nper = the total number of times interest is calculated
- pmt = the additional money you add each period
- pv = the present value, or the initial deposit. If you omit this, it’s assumed to be 0.
- type = either the number 0 or 1. 0 indicates payments are due at the end of the period while 1 indicates payments are due at the start of the period. If you omit this, it’s assumed to be 0.
If you leave out the pmt variable, you’ll get the same result as the first equation. To continue with the example above, here’s what would happen if you added $100 a month to your initial $5,000 deposit:
=FV(0.05/12,10*12,100,5000,0)
After 10 years at 5% interest, you would end up with about $23,763.
If you don’t want to do the math yourself, a compound interest calculator will do all of the work for you.
Here are the five key variables involved in understanding compound interest:
- Interest. This is the interest rate you earn or are charged. The higher the interest rate, the more money you earn or the more money you owe.
- Starting principal. How much money are you starting with? How big a loan did you take out? While compounding adds up over time, it’s all based on the initial amount you deposit or borrow.
- Frequency of compounding. The pace at which interest is compounded—daily, monthly or annually—determines how rapidly a balance grows. When taking out a loan or opening a savings account, make sure you understand how often interest compounds.
- Duration. How long do you anticipate owning an account or paying off a loan? The longer you leave money in a savings account or the longer you hold on to a debt, the longer it has to compound and the more you’ll earn—or owe.
- Deposits and withdrawals. Do you anticipate making regular deposits into your account? How often will you make loan payments? The pace at which you build up your principal balance or pay down your loan makes a big difference over the long run.
But more than anything else, the following three examples amplify the power of compounding:

The Wheat and a Chessboard is an ancient legend about the inventor of chess, who showed his invention to the Emperor of India for the first time. The Emperor was very impressed by the invention.
He liked it so much, that he offered any reward the inventor could wish for.
The inventor said: “My wish is very simple.
There are 64 squares on the chessboard and
for the first square I wish only 1 grain of wheat,
for the second one I wish 2 grains,
for the third one I wish 4 grains,
for the fourth I wish 8 grains,
for the fifth I wish 16 grains
and so on for all the 64 squares”.
The emperor was not good at math and was surprised that the inventor seemed to have asked for such a small reward.
So the Emperor ordered his treasurer to give the inventor the wheat grains for all the squares as requested.
A few days later the Emperor asked his treasurer whether the chess inventor has been rewarded.
The treasurer informed the emperor that the reward turned out to be an astronomical sum, greater than all the wheat that could be gathered in many centuries.
This legend illustrates how powerful the exponents can be.
Let’s go through the legend once again, but this time, we will look at how the numbers were calculated to determine the amount of wheat grains.
The following chessboard contains 64 squares and illustrates how many grains of wheat each square the inventor asked for represents.

If we look at the numbers on the squares, we can see that each subsequent square contains the number that is two times greater than the previous one.
This is an interesting example by Joel Darr on quora.comcom:
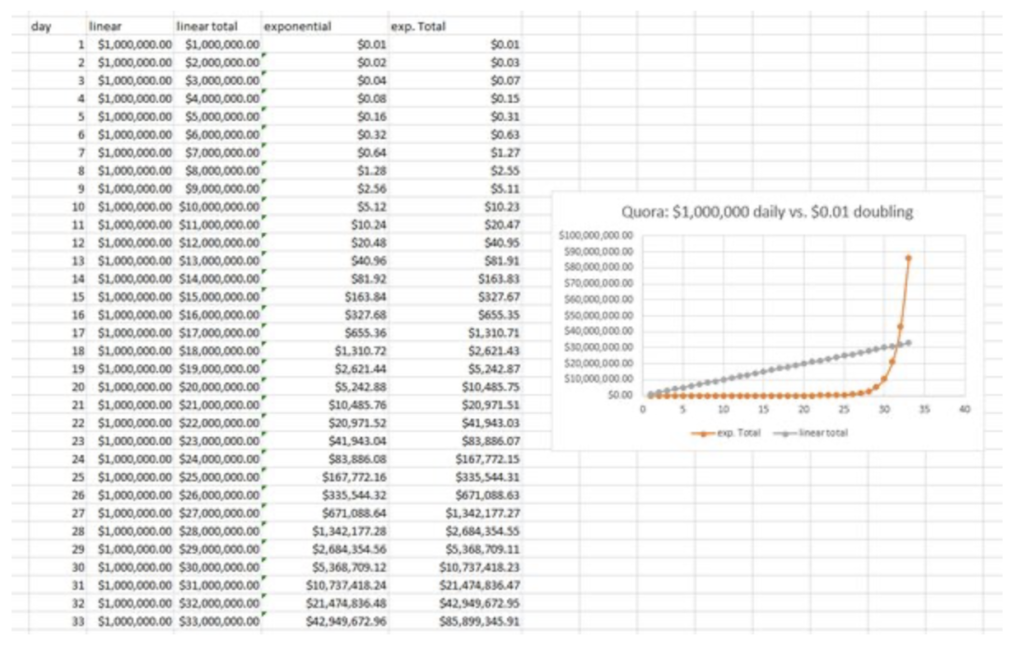
If it’s just a month, you’d want to take the cool daily million. Depending on the month, you’d end up with $28,000,000, $30,000,000, or $31,000,000. In the same amount of time with the penny doubling, you’d end up with either $2,684,354.55, $10,737,418.23 or $21,474,836.47. However, if you could get the wish granter to give you just one extra day (maybe promise them you’ll buy them several million dollars worth of leftover Halloween candy or something), doubling would be the way to go, with a total of $42,949,672.95 compared to $32,000,000.
Another favorite:
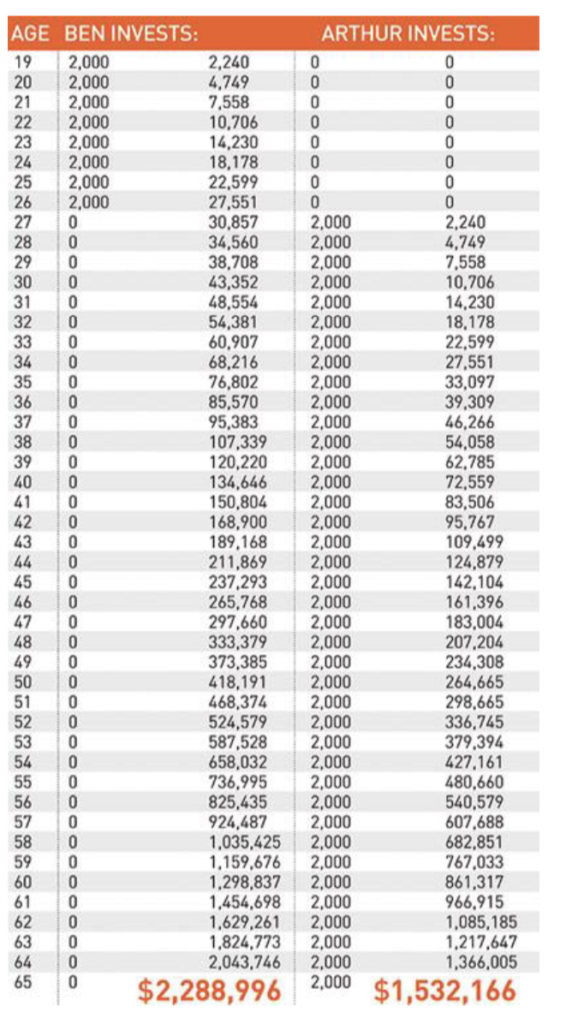
Ben and Arthur were friends who grew up together. They both knew that they needed to start thinking about the future. At age 19, Ben decided to invest $2,000 every year for eight years. He picked investment funds that averaged a 12% interest rate. Then, at age 26, Ben stopped putting money into his investments. So he put a total of $16,000 into his investment funds.
Now Arthur didn’t start investing until age 27. Just like Ben, he put $2,000 into his investment funds every year until he turned 65. He got the same 12% interest rate as Ben, but he invested 23 more years than Ben did. So Arthur invested a total of $78,000 over 39 years.
When both Ben and Arthur turned 65, they decided to compare their investment accounts. Who do you think had more? Ben, with his total of $16,000 invested over eight years, or Arthur, who invested $78,000 over 39 years?
Believe it or not, Ben came out ahead … $700,000 ahead! Arthur had a total of $1,532,166, while Ben had a total of $2,288,996. How did he do it? Starting early is the key. He put in less money but started eight years earlier. That’s compound interest for you! It turns $16,000 into almost $2.3 million! Since Ben invested earlier, the interest kicked in sooner.
Final Thoughts
*There are several key principles involved in the success of compound interest. *The most important factor is time. The greatest effects of compounding become most evident over longer time periods. *Larger initial deposits will yield greater final results. *The higher the interest rate, the greater the compounding and the more money you earn. *The more compounding periods (the frequency of compounding), the greater the returns. *Withdrawals will decrease the account balance and hurt long term returns.
Utilize Albert Einstein’s philosophy by investing as much money as possible at the highest interest rate available with the best compounding frequency over the longest time possible. If funds are added periodically and left in place, then you should create a sizable balance.
If you’d like to be a part of a free online retirement community, join us on Facebook:
COMMENTS